xi
fi
xifi
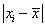
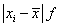
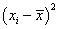
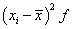
1
13
20
260
3,2
64
10,24
204,8
2
15
30
450
1,2
36
1,44
43,2
3
17
25
425
0,8
20
0,64
16
4
19
20
380
2,8
56
7,84
156,8
5
21
5
105
4,8
24
23,04
115,2
85
100
1620
12,8
200
43,2
536
Задача за 100 руб.
Для контроля за качеством поступившей партии товара произведено 5%-ное выборочное обследование. При отборе в выборку образцов по схеме механического отбора получены следующие данные о содержании влаги:| Влажность, % |
Количество образцов |
| До 14 |
20 |
| 14-16 |
30 |
| 16-18 |
25 |
| 18-20 |
20 |
| 20 и выше |
5 |
| Итого |
100 |
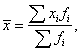
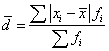
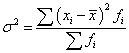
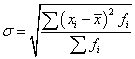
| xi |
fi |
xifi |
|
|
|
|
|
| 1 |
13 |
20 |
260 |
3,2 |
64 |
10,24 |
204,8 |
| 2 |
15 |
30 |
450 |
1,2 |
36 |
1,44 |
43,2 |
| 3 |
17 |
25 |
425 |
0,8 |
20 |
0,64 |
16 |
| 4 |
19 |
20 |
380 |
2,8 |
56 |
7,84 |
156,8 |
| 5 |
21 |
5 |
105 |
4,8 |
24 |
23,04 |
115,2 |
| 85 |
100 |
1620 |
12,8 |
200 |
43,2 |
536 |
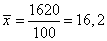
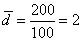
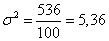
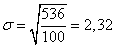
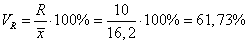
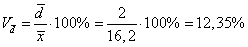
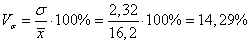
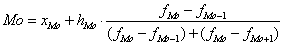
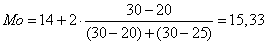
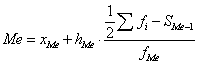
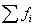 - сумма частот;
- сумма частот;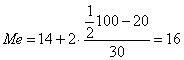
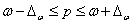
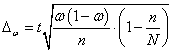 – предельная ошибка выборочной доли.
– предельная ошибка выборочной доли.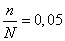
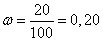 , вероятность равна 0,954, тогда t = 2
, вероятность равна 0,954, тогда t = 2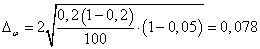
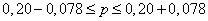
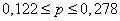
5. Установите с вероятностью 0,997 возможные пределы среднего процента влажности для всей партии товара
Предельную ошибку выборки рассчитаем по формуле
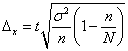 ,
,
где 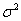 – дисперсия выборочной совокупности.
– дисперсия выборочной совокупности.
Т.к. вероятность равна 0,997, то t = 3, тогда предельная ошибка выборки равна
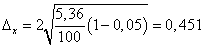 .
.
Следовательно, с вероятностью 0,954 можно утверждать, что разность между выборочными (обследованные образцы) и генеральными показателями не превысит 0,451%.
С помощью предельной ошибки выборки определим границы для среднего процента влажности для всей партии товара:
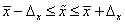 .
.
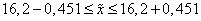
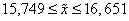
с вероятностью 0,997 можно ожидать, что средний процент влажности для всей партии товара будет в пределах от 15,7% до 16,7%.